Anderhalf miljard jaar geleden zijn op gigantische afstand van de aarde twee kolossale massa’s op elkaar gebotst. In ongeveer 200 milliseconden smolten de giganten, elk zo groot als de provincie Zeeland en elk ongeveer 30 keer zo zwaar als onze zon, samen tot één zwart gat. Bij de botsing kwam heel kort vijftig keer meer energie vrij dan al het licht van alle sterren in het heelal. Een dergelijke gebeurtenis heeft zogenaamde zwaartekracht-golven tot gevolg. 

Zwaartekracht-golven werden 100 jaar geleden voorspeld door de zogenaamde Algemene Relativiteitstheorie. Deze theorie voorspelde dat veranderingen in de zwaartekracht rimpelingen in de ruimte en de tijd (ja, zelfs de tijd!) veroorzaken. De twee zware massa’s waar we het nu over hebben botsten anderhalf miljard jaar geleden met elkaar en sinds dat moment liepen de daardoor ontstane zwaartekracht-rimpels door het heelal. Net als rimpelingen in een vijver waarin je een steen gooit werden ze over een steeds groter gebied uitgesmeerd, en verzwakten daardoor. Het heelal bestaat dan weliswaar niet uit water, maar toch blijkt een verplaatsing van massa - ergens in het heelal, vele miljarden kilometers verder en vele miljarden jaren later - andere massa’s in beweging te kunnen brengen. 

En vorig jaar kwamen die zwaartekracht-golven aan bij de aarde, al merkte die daar nauwelijks wat van want daar is de kracht te klein voor. Maar ze werden - nu voor het eerst en ook een beetje door mazzel - opgemerkt door twee meetinstrumenten, samen LIGO geheten: Laser Interferometer Gravitational Wave Observatory. De ene staat in Hanford, Washington, de ander in Livingston, Louisiana.. Zo’n 4000 kilometer van elkaar. Die grote afstand is noodzakelijk zoals zometeen duidelijk zal worden.

Over Ruimte, Tijd en Ruimtetijd

De relativiteitstheorie stelt dat zowel de ruimte als de tijd geen absolute begrippen zijn. Dat is lastig voor te stellen, maar het blijkt zo te zijn dat de lengte van een stok anders blijkt te zijn wanneer je daar met verschillende snelheden langs reist. Ook is inmiddels aangetoond dat een klok langzamer loopt als je sneller gaat reizen. Sterker nog: die klok staat zelfs stil als je met de lichtsnelheid zou reizen. Omdat deze effecten pas echt gaan meetellen bij zeer, zeer hoge snelheden (bijvoorbeeld vanaf de halve lichtsnelheid) merken wij op aarde daar vrijwel niets van, maar daar wordt het principe niet anders van). Wanneer hierna gesproken wordt over Ruimtetijd (ook wel Tijdruimte genoemd) moet je dat in gedachten houden.

Persoonlijk vind ik het begrip ’Ruimtetijd’ nodeloos verwarrend en ik zou het liever gewoon ’Ruimte’ blijven noemen, zolang we maar in de gaten houden dat het begrip ’tijd’ daar een onlosmakelijk deel van uitmaakt.

Zie mijn toelichting aan het eind van dit artikel.

Wat zijn zwaartekracht-golven?

Twee massa’s trekken elkaar aan. Hoe groter een massa, hoe groter zijn aantrekkingskracht op een andere massa. De massa’s kunnen zwarte gaten zijn, of de aarde en de zon. Ook een melkbeker op de ontbijttafel en het ontbijtbord, trekken elkaar aan, maar omdat de aantrekking van de aardmassa zo veel groter is wint die het royaal en merken mok en bord vrijwel niets van elkaar.

Elke concentratie van massa ’kromt’ de ruimtetijd ter plaatse, zoals ook die melkbeker een heel klein deukje in het tafelkleed maakt. Als er verder niets gebeurt met die massa’s zijn er ook geen rimpelingen, maar zodra de plaats van een massa ten opzichte van andere massa’s verandert dan ontstaat een rimpeling in de ruimte en de tijd. Die rimpeling heet een zwaartekracht-golf. En die rimpeling heeft invloed op de plaats en de beweging van massa’s in zijn omgeving. 

Er is niets op tegen om dat te vergelijken met een vijver waarin een paar vissen roerloos liggen tot een van die vissen met zijn staart slaat. Daardoor ontstaat een rimpeling in het water. Door die rimpeling gaat een vis die verderop nog roerloos ligt te wachten, dus een beetje mee op en neer bewegen. (Dit nu is een drie dimensionaal voorbeeld, en het is lastig om dit voor te stellen in een dimensietje meer, maar wiskundig is dit gelukkig geen enkel probleem), 

Een bewegende - of zich verplaatsende - massa heeft in de ruimtetijd ook een vergelijkbare rimpeling tot gevolg. Waarom kunnen wij mensen dat zo moeilijk meten?

Een rimpeling in de ruimte/tijd ten gevolge van een massaverplaatsing heeft ten eerste een heel lage frequentie. Dat wil zeggen de afstand van de verschillende golven in die vijver (het heelal) is erg groot. Maar daar komt nog eens bij bij dat de amplitude ervan (de hoogte van de golven in de vijver) heel klein is. 

Kortom: omdat de effecten voor menselijke begrippen uiterst zwak zijn, is het voor ons heel lastig om die effecten te meten.

Die rimpelingen zijn zwaartekracht-golven. Einstein voorspelde ze in 1916, maar dacht dat ze wel nooit te meten zouden zijn. Zelfs de extreem krachtige golven van botsende zwarte gaten leiden tot een uiterst kleine vervorming, te vergelijken met de verhouding van een haardikte ten opzichte van 40.000 miljard kilometer

Hoe worden Zwaartekracht-rimpels gemeten?

Zoals gezegd zijn de effecten van zwaartekracht-rimpels eigenlijk domweg te klein om met gewone meetinstrumenten te kunnen vinden. Om die toch te kunnen meten moet dus een truc verzonnen worden. En die truc was om die rimpel-gevolgen als het ware te versterken. In het dagelijks leven kan je iets heel zwaars optillen door een koevoet (een hefboom) te gebruiken. Dwz. de ’arm’ waar je op drukt te verlengen ten opzichte van het steunpunt. Daarvoor is voor dit zwaartekracht- onderzoek een zogenaamde interferometer gebruikt. Om precies te zijn twee stuks op een afstand van zo’n 4000 kilometer van elkaar.

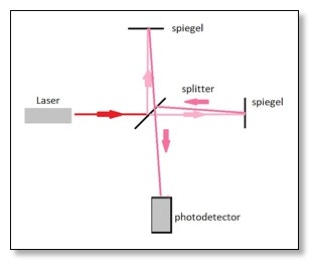
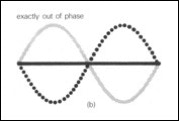
Elk van deze twee interferometers bestaat uit een laser die zijn bundel stuurt naar een ’splitter’. Daardoor wordt de straal in twee gelijke delen verdeeld die m.b.v spiegels in twee richtingen wordt gestuurd. Elke bundel legt dan een zekere afstand af waar hij door een andere spiegel wordt teruggestuurd naar de splitter. Omdat licht zich als een golf gedraagt en beide bundels in principe qua golfgedrag identiek zijn kun je de spiegels zo plaatsen dat het teruggekaatste laserlicht van de ene bundel precies een golf berg omhoog heeft waar de andere een golfberg omlaag heeft (zie figuur) 

Dat heet ’tegenfase’. Wanneer deze twee laserstralen bij het splitsingspunt weer bij elkaar komen zullen de twee tegengestelde lichtgolven elkaar opheffen en zal het donker zijn. En heel kleine beweging van de ene spiegel ten opzichte van de ander zal dit proces verstoren en er zal onmiddellijk dus een klein beetje licht te meten zijn (met een photodetector, zie plaatje) omdat de berg up en de berg down elkaar niet meer exact opheffen. 

Hoe groter de afstand die de bundels afleggen tussen de splitter en de terugkaats-spiegel hoe duidelijker zal dat te zien zijn (koevoeteffect). In de gebruikte apparatuur in Amerika was die afstand 4 kilometer per gesplitste laserstraal. Dus elke interferometer moet een uitgestrekt apparaat (4 km) zijn om überhaupt iets te kunnen meten. Met deze koevoet-truc kan iets gezegd worden over de amplitude (de hóógte van de golf in de vijver). 

Maar de àfstand tussen beide interferometers moet eveneens enorm zijn (4000 km: dus nòg een keer het koevoet-effect) om kleine verschillen in meetwaarden tussen beide te kunnen zien. (Vergelijk: de afstand tussen de rimpelingen in de vijver.) 

Even terzijde: Vanzelfsprekend zijn alle spiegels zo opgehangen dat zij ongevoelig zijn voor trillingen in het aardoppervlak. Dat is lastig maar dat is te doen… Ze hangen dus doodstil te wachten totdat een of andere kracht van buitenaf ze zal doen bewegen.

Welnu, de zwaartekracht-rimpeling van die versmelting van die twee zware massa’s deed de spiegels van beide interferometers inderdaad even trillen, maar kort na elkaar. Alsof de rimpel in de vijver inderdaad eerst de ene en even later de andere interferometer bereikt. En dat was het bewijs! Overigens was de trilling een duizendste van de dikte van een atoomkern. Maar dankzij de grote afstanden tussen de apparaten bleek het genoeg om een uitspraak te kunnen doen over het passeren van een zwaartekracht-golf.

Er zijn nu plannen om over 20 jaar een stelsel van grote interferometers in de ruimte te brengen waardoor de koevoet-arm uitgebreid kan worden tot een paar miljoen kilometer (in plaats van de 4000 kilometer die nu gebruikt werd). De gedachte is dat op die manier als het ware de ene zwaartekracht rimpeling na de andere te meten is en de hoop bestaat we dan ineens door een heel andere bril kunnen gaan kijken naar het ’gedrag’ van massa’s in het heelal.

waarom willen we dit eigenlijk weten?

De natuur kent een aantal fundamentele ’krachten’ waarmee het verband en de wisselwerking tussen zaken heel best begrepen kunnen worden. Om maar een heel eenvoudig voorbeeld te noemen: het verband tussen magnetische en electrische krachten. De ouderwetse fietsdynamo is daarvan een prachtig voorbeeld: Draai een magneet rond in een lusvormig electrisch draadje en als gevolg daarvan gaat er in dat draadje een stroompje lopen waarop een lampje kan branden.

Ook andere - maar voor leken veel lastiger te begrijpen - krachten kunnen als het ware in elkaar worden uitgedrukt. Anders gezegd: je kunt het branden van dat lampje net zo makkelijk beschrijven in termen van magnetisme als van electriciteit. Het is maar wat je op zeker moment het beste uitkomt. 

Maar het gedrag van de zwaartekracht is tot nu in dat geheel eigenlijk niet in te passen terwijl natuurkundigen van mening zijn dat gewoon op basis van logisch redeneren dat wel zou moeten. Als ALLE krachten in de natuur energie in elkaar kunnen overdragen behalve de zwaartekracht is dat gewoon niet logisch. De vraag is alleen HOE. 

Nog een mooi voorbeeld: de zwaartekracht is een fenomeen dat zich afspeelt in en rond heel grote massa’s. De quantum mechanica is daarentegen een fenomeen dat pas betekenis krijgt in de allerkleinste deeltjes die wij kennen. De gedachte is nu dat bij het ontstaan van het heelal alle massa van het heelal zich bevond in een volume kleiner dan een atoom (moeilijk voor te stellen, maar daar gaat het nu niet om). Dan zou daar de quantummechanica en de zwaartekrachten elkaar moeten treffen. Een relatie die nauwelijks is voor te stellen, maar zuiver theoretisch denkbaar is. (volgens mij heeft Stephen Hawking dit idee voor het eerst geopperd). 

En Erik Verlinde zegt nu dat Zwaartekracht misschien wel helemaal geen 'kracht' is, maar dàt is wat mensen ervaren als er 'informatie-verschillen' tussen massa's bestaan. (hmmm, lastig te begrijpen hoor)

.